The Role of Markov Chains in Machine Vision Systems
Markov chain machine vision systems play a vital role in enabling intelligent decision-making based on sequential data. These mathematical models help such systems predict the next state of an object or event using probabilities derived from previous states. For example, researchers developed three Markov chain machine vision system models to analyze student performance in visual learning environments. They found that one group achieved a 90.0% likelihood of advancing in ability, compared to 63.0% and 42.1% for others. This shows how Markov chain machine vision systems can evaluate actions and predict outcomes, making them essential in visual data analysis.
Key Takeaways
- Markov chains guess what happens next using current information. This helps with tasks like finding objects and moving around.
- Transition matrices show chances of changes, helping AI predict moves in busy places like traffic.
- Combining Markov chains with deep learning makes decisions better. This helps in medical pictures and self-driving cars.
- Markov chains make hard visual data easier to understand. This allows quicker work and real-time use.
- These models can grow big, so they work well with large data and tricky AI tasks. They give good guesses in many situations.
Fundamentals of Markov Chains in Computer Vision
Definition and Key Concepts
Markov chains are mathematical systems that model sequences of events where the probability of each event depends only on the state of the previous one. In computer vision, these systems help you analyze and predict patterns in visual data. For example, when processing images, a Markov chain can determine the likelihood of a pixel belonging to a specific object based on its neighboring pixels. This makes it a powerful tool for tasks like object detection and recognition.
Markov chains rely on a concept called the "Markov property," which assumes that the future state depends solely on the current state, not the sequence of events that preceded it. This simplicity allows you to build efficient models for analyzing complex visual data. These models are particularly useful in stochastic environments, where randomness plays a significant role, such as in real-time video analysis or augmented reality applications.
Key applications of Markov chains in computer vision include generating realistic images, enhancing augmented reality experiences, and improving text prediction in generative AI models. For instance, they are integral to AI systems that process images in virtual reality (VR) and augmented reality (AR) environments. By leveraging the Markov process, these systems can simulate realistic transitions between visual states, creating seamless user experiences.
Transition Matrices in Machine Vision
A transition matrix is a core component of any Markov chain. It represents the probabilities of moving from one state to another. In machine vision, this matrix helps you model how visual elements change over time or across frames in a video. For example, in self-driving cars, transition matrices predict the movements of other vehicles and pedestrians, enabling real-time decision-making.
Imagine a scenario where an AI system analyzes a video of traffic. The transition matrix might show a high probability of a car moving forward and a lower probability of it turning left. This information allows the AI to anticipate actions and adjust its behavior accordingly. Transition matrices are also used in medical imaging to track changes in tissue over time, improving disease detection accuracy by up to 20% (Wu et al., 2019).
The simplicity of transition matrices makes them scalable for complex AI systems. You can use them to model interactions between multiple objects in a scene, such as tracking the movement of players in a sports video. This scalability ensures that Markov chain machine vision systems remain efficient even when analyzing large datasets or high-resolution images.
Decision-Making Models for AI Applications
Markov chains play a crucial role in decision-making models for AI applications. These models use probabilities to evaluate different outcomes and select the most likely or optimal one. In computer vision, this capability is essential for tasks like object detection, pattern recognition, and real-time navigation.
For example, in autonomous vehicles, Markov chains help AI systems decide how to respond to dynamic environments. They predict the behavior of other road users and adjust the vehicle's path to avoid collisions. Similarly, in medical imaging, decision-making models powered by Markov chains assist in diagnosing diseases by analyzing patterns in visual data.
The effectiveness of these models can be measured using various performance metrics. For instance:
| Metric Type | Description |
|---|---|
| Business Impact Metrics | Measure AI’s contribution to strategic goals, such as adoption rate and revenue growth. |
| Model Performance Metrics | Assess internal efficacy and decision reliability, including metrics like F1 score and error rate. |
| Operational KPIs | Ensure stable AI deployment and user experience, tracking response time and throughput. |
| Risk & Governance Metrics | Monitor ethical AI use, including compliance rates and data privacy scores. |
These metrics highlight the reliability and scalability of Markov chain-based decision-making models. By integrating these models with deep learning and neural networks, you can create AI systems that excel in both accuracy and efficiency.
Applications of Markov Chains in AI and Vision Systems
Medical Imaging and Diagnostics
Markov chains have transformed medical imaging by enabling precise analysis of complex visual data. You can use these models to predict disease progression and improve diagnostic accuracy. For instance, researchers combined Markov models with MR diffusion tensor imaging to forecast the onset of Alzheimer’s disease. These models incorporated patient-specific transition rates, regional volumetric data from MRI scans, cognitive scores, and demographics. This approach ensures that predictions are tailored to individual patients, enhancing reliability.
In prostate cancer diagnosis, Markov chains play a crucial role in understanding disease dynamics. A probability matrix derived from the Markov transition chain outlines the likelihood of various end states, helping you interpret the progression of the disease. The positive predictive value of these models reaches 0.93 (95% CI 0.72–0.99), demonstrating their effectiveness in identifying cancerous tissues.
Tip: By integrating Markov chains with AI models, you can achieve real-time analysis of medical images, enabling faster and more accurate diagnoses.
Autonomous Vehicles and Navigation
Markov chains are essential for autonomous vehicles, helping them navigate dynamic environments with precision. These models predict the behavior of other road users, such as cars and pedestrians, based on their current states. For example, a Markov chain machine vision system can analyze traffic patterns and anticipate movements, allowing vehicles to make safe decisions in real-time.
You can also use Markov chains to optimize navigation routes. By modeling the probabilities of different paths, these systems identify the most efficient route while avoiding obstacles. This capability is particularly useful in urban areas, where traffic conditions change rapidly. The integration of Markov chains with deep learning and neural networks enhances the system’s ability to process large volumes of visual data, ensuring accurate predictions and smooth navigation.
Note: Autonomous vehicles rely on Markov processes to adapt to stochastic environments, making them safer and more reliable.
Image Processing and Pattern Recognition
Markov chains excel in image processing and pattern recognition by modeling the relationships between pixels. You can use Markov Random Fields (MRFs) to generate stochastic image models, where the intensity of a pixel depends on its neighbors. This approach is ideal for tasks like object detection and recognition, as it captures the spatial dependencies within images.
MRFs utilize Gibbs distributions represented through Feynman graphs, providing a flexible framework for stochastic modeling. These models have demonstrated applications in image processing using stochastic differential equations driven by Lévy noise. For example, you can apply them to enhance generative AI models, creating realistic images and improving text prediction capabilities.
In addition, Markov chains streamline pattern recognition by analyzing visual data in real-time. They identify recurring patterns and classify objects with high accuracy, making them invaluable for applications like facial recognition and security systems.
Callout: By leveraging Markov chains, you can build AI systems that process images efficiently, even in high-resolution formats.
Benefits of Markov Chains in Machine Vision Systems
Predictive Capabilities in Computer Vision
Markov chains enhance predictive capabilities in computer vision by analyzing sequential data and forecasting future states. You can use these models to predict the movement of objects in dynamic environments, such as vehicles or pedestrians in traffic. This ability makes them essential for applications like autonomous navigation and real-time surveillance.
For example, in object detection tasks, Markov chains evaluate the likelihood of an object appearing in a specific location based on its previous positions. This predictive approach improves accuracy and speeds up decision-making processes. By leveraging the Markov process, you can create systems that anticipate changes in visual data, enabling smoother transitions and better outcomes in real-time applications.
Tip: Use Markov chains to enhance prediction in stochastic environments, where randomness affects visual data patterns.
Efficiency in Visual Data Analysis
Markov chains streamline visual data analysis by simplifying complex relationships between elements in images or videos. These models focus on the current state of visual data, reducing computational overhead and improving processing speed. You can apply them to tasks like image segmentation, where they classify pixels based on their neighbors, ensuring efficient and accurate results.
In medical imaging, Markov chains analyze tissue changes over time, enabling faster disease detection. Their efficiency also extends to generative AI models, where they help create realistic images by modeling pixel dependencies. By integrating Markov chains with deep learning and neural networks, you can achieve high-performance systems that process large datasets without compromising speed or accuracy.
Callout: Markov chains reduce the complexity of visual data analysis, making them ideal for real-time applications in AI systems.
Scalability for Complex AI Systems
Markov chains offer scalability for complex AI systems, allowing you to model interactions between multiple agents or objects. Research demonstrates their effectiveness in large-scale applications, such as decentralized policy optimization frameworks. These frameworks use Markov chains to estimate global information accurately while maintaining performance with limited data samples.
In multi-agent systems, Markov chains enable coordination among hundreds of agents, ensuring reliable predictions and efficient decision-making. You can deploy these models in real-world scenarios, such as traffic management or crowd analysis, where scalability is crucial. Their ability to handle vast amounts of visual data makes them indispensable for AI applications requiring high levels of complexity and precision.
Note: Scalability ensures that Markov chain machine vision systems remain effective even in demanding environments with large datasets.
Challenges and Solutions in Markov Chain Machine Vision System
Computational Complexity and Optimization
Markov chain machine vision systems often face computational complexity due to the large datasets and intricate models required for analyzing visual data. You can address this challenge by optimizing deep learning models. Studies show that optimized models are 7.011× faster than non-optimized ones, making them suitable for time-sensitive applications like real-time object detection. Tools like TensorRT reduce inference time, ensuring faster processing without compromising accuracy.
To further enhance performance, you can explore optimization strategies such as Stochastic Gradient Descent (SGD) and Adam optimizer. Research highlights that the Adam optimizer achieved 97.30% accuracy in skin cancer detection tasks, demonstrating its effectiveness in improving model performance. By analyzing optimization techniques, you can guide future work in machine learning and computer vision applications.
Tip: Focus on reducing FLOPS (floating-point operations per second) to manage computational complexity effectively.
Fine-Tuning Models for Accuracy
Fine-tuning models is essential for achieving high accuracy in Markov chain-based systems. Controlled experiments reveal how adjustments in episode length and MCMC steps impact performance metrics like EER and SBERT scores. For example, increasing MCMC steps to 100% improves accuracy, with EER reaching 0.224 and SBERT scoring 0.835.
| Episode length | EER↑↑ | SBERT↑↑ |
|---|---|---|
| 2 | 0.132 | 0.923 |
| 5 | 0.224 | 0.835 |
| 8 | 0.200 | 0.745 |
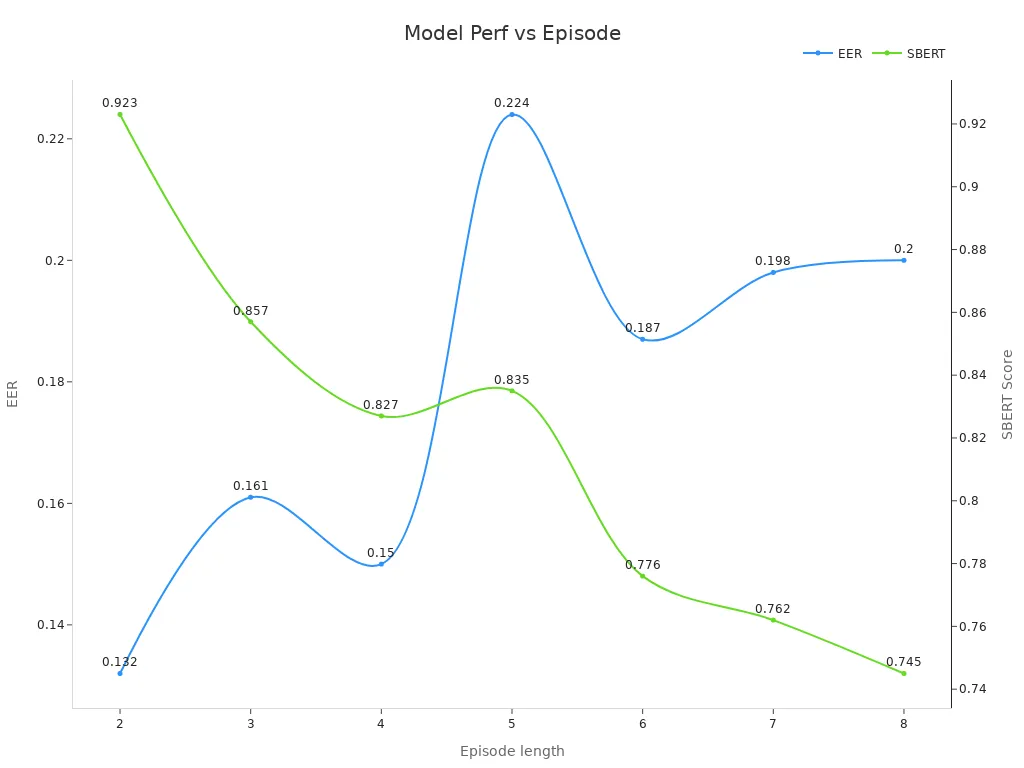
By fine-tuning parameters like episode length and MCMC steps, you can improve the accuracy of Markov chain models in applications such as generative AI models and neural networks.
Managing Uncertainty in Visual Data
Uncertainty in visual data poses a significant challenge for Markov chain machine vision systems. You can manage this by classifying indeterminate cases and using probability distributions to assign results. For example, when diagnosing medical images, you can report results as positive or negative while providing the associated probability of accuracy.
Markov chains excel in handling stochastic environments, where randomness affects visual data patterns. By leveraging the Markov process, you can create systems that adapt to uncertainty and provide reliable predictions. This approach is particularly useful in applications like real-time surveillance and autonomous navigation, where accurate decision-making is critical.
Callout: Use probability density mass to improve the reliability of predictions in uncertain scenarios.
Markov chains play a pivotal role in machine vision systems by enabling accurate predictions and efficient visual data analysis. You can see their impact in applications like autonomous navigation, medical imaging, and pattern recognition, where they enhance decision-making and streamline processes. These models contribute significantly to advancing AI technologies, offering scalable solutions for complex systems and improving real-time performance.
Ongoing research highlights promising developments, such as hardware-based Markov chain algorithms that simplify system design and expand practical applications. This trend signals a growing interest in leveraging Markov chains to address challenges in machine vision. As researchers continue to innovate, you can expect these systems to unlock new possibilities in AI and computer vision.
FAQ
What are Markov chains, and why are they important in machine vision?
Markov chains are mathematical models that predict future states based on current ones. They simplify complex visual data analysis by focusing on probabilities. You can use them to enhance tasks like object detection, navigation, and medical imaging, making AI systems more efficient and accurate.
How do Markov chains handle uncertainty in visual data?
Markov chains manage uncertainty by assigning probabilities to outcomes. This helps you classify ambiguous cases and make reliable predictions. For example, in medical imaging, they provide confidence levels for diagnoses, ensuring accurate results even when data contains randomness or noise.
Can Markov chains work with deep learning models?
Yes, Markov chains integrate seamlessly with deep learning. You can combine them to improve decision-making and prediction accuracy. For instance, they enhance neural networks by modeling sequential data, enabling applications like autonomous navigation and real-time video analysis.
What are transition matrices, and how do they help in machine vision?
Transition matrices represent probabilities of moving between states. In machine vision, they model changes in visual elements over time. You can use them to predict object movements, track patterns, or analyze dynamic environments like traffic or sports videos.
Are Markov chains scalable for large datasets?
Markov chains scale well for large datasets. Their simplicity allows you to model interactions between multiple objects efficiently. This makes them ideal for complex AI systems, such as multi-agent simulations or high-resolution image processing, without compromising performance.
Tip: Use Markov chains for real-time applications where scalability and speed are critical.
See Also
A Comprehensive Guide to Computer And Machine Vision
The Role of Synthetic Data in Machine Vision
An Overview of Thresholding Techniques in Machine Vision
